탐욕 알고리즘
탐욕 알고리즘은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다. 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다.
출처: 위키피디아
탐욕 알고리즘은 지역적으로 최적인 선택을 계속 이어나가서 전역적 해답을 얻는 방식의 알고리즘이다.
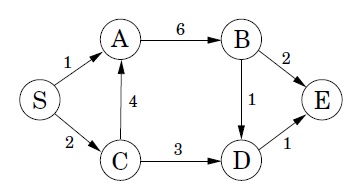
위와 같은 그래프의 S 에서 E 까지 도달할 수 있는 방법 중 가중치 합이 가장 낮은 방법을 찾는데에 탐욕 알고리즘을 쓴다면 S -> A -> B -> D -> E 의 경로를 선택하게 될 것이다. S 에서 A 로 가는 것이 이 후의 선택에서 어떤 영향을 미치게 될지는 고려하지 않고 그냥 단순히 그때 그때의 상황에서 가장 가중치가 낮은 길로만 진행하는 것이다. 이런 방식으로 찾은 해는 대부분의 경우 최적해가 아니다. 하지만 탐욕 알고리즘의 진가는 고려해야하는 경우의 수가 너무 많아서 최적해를 찾아내는데 너무나 오래걸리는 문제가 있을 때 이 문제의 최적해에 어느 정도 근접하는 해를 찾을 때 발휘된다!
가방 채우기 문제
어떤 도둑이 총 35 파운드까지만 담을 수 있는 가방을 가지고 물건을 훔치려고 한다고 생각해보자.
훔치는 물건의 가치가 최대가 되기 위해서는 어떤 물건들을 훔쳐야할까?
도둑이 훔칠 수 있는 물건이 다음의 세 개라고 가정해보자.
스피커
$3000
30 파운드
노트북
$2000
20 파운드
모니터
$1500
15 파운드
이 때, 가방에 담을 수 있는 물건들의 가치를 최대로 하려면 노트북 과 모니터 를 담아서 총 가치가 $3500 가 되게 하면 될 것이다. 그런데 만약 도둑이 훔칠 수 있는 물건이 세 개가 아니라 수십가지가 있다면 어떨까? 가장 최적의 답을 찾으려면 가방이 담을 수 있는 무게를 모두 채울 수 있는 물건들의 모든 경우의 수를 찾아서 비교를 해보아야할 것이다. 실제로 그러고 있다가는 경찰에 잡히고 말 것이다.
이런 경우에 탐욕 알고리즘을 통해 문제를 풀어보면 어떨까? 탐욕 알고리즘을 사용하면 다음의 단계를 통해서 답을 찾을 수 있다.
- 가장 가치가 높은 물건을 가방에 담는다.
- 남은 가방 공간에 들어갈 수 있는 물건들 중 가장 가치가 높은 물건을 담는다.
단계 2반복
훔칠 수 있는 물건이 세 개인 경우에 탐욕 알고리즘에 따라 물건을 담으면 처음에 가장 가치가 높은 스피커 를 담게 될 것이다. 그러면 담을 수 있는 무게가 5 파운드 남게되지만 남은 물건들이 모두 5파운드 보다는 무겁기 때문에 더 담을 수 없게된다. 이렇게 탐욕 알고리즘을 통해 얻은 이 답은 최적의 답이 아니게 된다. 하지만 여전히 $3000 으로 최적의 답인 $3500 에 꽤 근접한 답을 얻긴 했다. 만약 훔칠 수 있는 물건들이 훨씬 많았다면 어땠을까? 가장 최적의 답을 얻지는 못하겠지만 최적의 답에 꽤나 가까운 답을 모든 경우를 따져보며 찾을 때보다 훨씬 빠른 속도로 얻어낼 수 있게 될 것이다.
실제로 도둑이 물건을 훔칠 때는 담을 수 있는 가장 비싼 물건들의 조합을 생각하며 훔치기보다는 최대한 빨리 돈 될만한 것들 가능한 많이 챙겨서 나오기를 원할 것이다.
집합 커버링 문제
미국 50개 주에 있는 모든 사람들에게 라디오 쇼를 들려주려고 한다. 라디오 쇼를 송출하려면 방송국을 찾아가야 하는데 각 방송국이 담당하는 지역은 한정되어 있기 때문에 모든 주에 방송을 하려면 여러 방송국들을 방문해야한다. 이 때 각 방송국이 담당하는 주가 최대한 겹치지 않도록 하면서 최대한 적은 수의 방송국을 방문하도록 하려면 어떻게 해야할까?
| 방송국 | 담당 주 |
|---|---|
| K-1 | 아이다호, 네바다, 유타 |
| K-2 | 워싱턴, 아이다호, 몬타나 |
| K-3 | 오레곤, 네바다, 캘리포니아 |
| K-4 | 네바다, 유타 |
| K-5 | 캘리포니아, 아리조나 |
| ... | ... |
이 문제를 불려면 먼저 가능한 모든 방송국들의 부분 집합을 다 나열해야한다. 이 때 가능한 부분 집합 수는 n 이 방송국 개수라고 할 때 \( 2^{n} \) 개이다.
이 부분 집합들 중 모든 주를 다 커버하면서 동시에 방문해야하는 방송국 수가 가장 적은 부분 집합을 골라야한다.
문제는 나열해야하는 부분 집합의 수가 \( 2^{n} \) 개이기 때문에 이 방법으로 문제를 푸는데 \( O(2^{n}) \) 시간이 걸린다는 점이다. 만약 초당 10개의 부분 집합을 확인할 수 있다면 방송국 수에 따른 알고리즘 실행시간은 아래와 같다.
| 방송국 수 | 실행 시간 |
|---|---|
| 5 | 3,2초 |
| 10 | 102.4초 |
| 32 | 13.6년 |
| 100 | 약 4,000,000,000,000,000,000,000년 |
더 절망적인 것은 이런 문제를 해결할 수 있는 더 빠른 알고리즘이 아직까지는 없다는 점이다. 이 때 탐욕 알고리즘을 사용하면 훨씬 빠른 속도로 최적해에 가까운 답을 찾아낼 수 있게 된다.
근사 알고리즘
위의 방송국 문제의 경우 탐욕 알고리즘을 대신 사용해서 최적해에 근사한 해를 빠른 속도로 계산해낼 수 있다.
- 먼저 가장 많은 지역을 담당하고 있는 방송국을 방문한다.
- 남은 지역들 중 가장 많은 지역을 담당하고 있는 방송국을 방문한다.
- 모든 주에 방송이 될 때까지 단계 2를 반복한다.
이렇게하면 가장 최적의 해를 구하는 경우보다는 훨씬 빠르게 상당히 최적해에 가까운 해를 찾을 수 있게된다. 이렇게 근사해를 찾는 알고리즘을 근사 알고리즘 (Approximation Algorithm) 이라고 한다.