다익스트라 알고리즘

06 Mar 2018

Reading time ~3 minutes

다익스트라 알고리즘

컴퓨터 과학에서, 데이크스트라 알고리즘(=다익스트라 알고리즘)(영어: Dijkstra algorithm)은 어떤 변도 음수 가중치를 갖지 않는 유향 그래프에서 주어진 출발점과 도착점 사이의 최단 경로 문제를 푸는 알고리즘이다. 이름은 네덜란드의 컴퓨터과학자 에츠허르 데이크스트라의 이름에서 유래했다. 예컨대 어떤 그래프에서, 꼭짓점들이 각각 도시를 나타내고, 변들이 도시 사이를 연결하는 도로의 길이를 나타낸다면, 데이크스트라 알고리즘을 통하여 두 도시 사이의 최단 경로를 찾을 수 있다.

데이크스트라 알고리즘은 방향이 주어진 가중 그래프(weighted graph) G와 출발점 s를 입력으로 받는다. 그래프 G의 모든 꼭짓점들의 집합을 V라 하고, 그래프의 변을 출발점 u와 도착점 v의 순서쌍 (u, v)로 표현한다. G의 모든 변들의 집합을 E라 하고, 변들의 가중치는 함수 w: E → [0, ∞]로 표현한다. 이때 가중치 w(u, v)는 꼭짓점 u에서 꼭짓점 v로 이동하는 데 드는 비용(시간, 거리 등)이 된다. 경로의 비용은 경로 사이의 모든 변들의 가중치의 합이 된다. 데이크스트라 알고리즘은 V의 임의의 꼭짓점의 쌍 s와 t가 있을 때 s에서 t로 가는 가장 적은 비용이 드는 경로(최단 경로)를 찾는다. 이 알고리즘은 주어진 출발점 s로부터 다른 모든 꼭짓점까지의 최단 경로를 계산하는 데도 사용할 수 있다.

출처: 위키피디아

다익스트라 알고리즘 (Dijkstra's algorithm) 은 그래프의 어느 한 노드에서 다른 한 노드로 가는 가장 빠른 길을 구할 때 사용할 수 있는 알고리즘이다. 너비 우선 탐색 (BFS) 과 다른점은 노드와 노드를 잇는 각각의 엣지들이 가중치를 가지는 그래프 (weighted graph)에서의 가장 빠른 길을 찾는다는 점이다. 단, 가중치가 음수인 경우에는 다익스트라 알고리즘을 사용할 수 없다. 따라서, 가장 빠른 시간 등과 같은 음수 가중치가 없는 상황에 적합한 알고리즘이다. 음수 가중치가 있는 그래프에는 벨만-포드 알고리즘 (Bellman-Ford algorithm) 을 사용하여 최단 거리를 구할 수 있다.

알고리즘 실행 단계

1단계: 한 노드에서 도달할 수 있는 노드 중 가장 적은 비용이 드는 노드를 찾는다.
2단계: 그 노드의 이웃 노드들에 도달하는데 드는 비용을 계산한다.
3단계: 1, 2단계를 그래프의 모든 노드들에 반복한다.
4단계: 최종 경로를 계산한다.

파이썬으로 구현

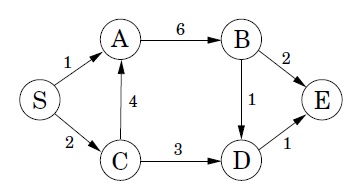
아래 예제 그래프의 S 에서 E 까지 가는 최단 경로를 파이썬으로 구현한 다익스트라 알고리즘으로 구해보자.

우선 3개의 해시 테이블을 생성해야한다.

그래프 테이블
비용 테이블
부모 테이블

그래프 테이블

먼저 그래프 테이블을 생성해주면 다음과 같다.

graph = dict()

# 시작점
graph['S'] = {}

# A 와 B 사이의 엣지 가중치
graph['S']['A'] = 1

# A 와 C 사이의 엣지 가중치
graph['S']['C'] = 2

A 노드의 모든 이웃 노드들은 다음과 같이 얻을 수 있다.

graph['S'].keys()

['A', 'C']

A 에서 B 로 가는 엣지의 가중치는 다음과 같이 얻을 수 있다.

graph['A']['C']

이런 식으로 모든 노드들을 해시 테이블로 생성해준다.

graph = {}

# 시작점 노드
graph['S'] = {}
graph['S']['A'] = 1
graph['S']['C'] = 2

# 노드 A
graph['A']['B'] = 6

# 노드 B
graph['B']['D'] = 1
graph['B']['E'] = 2

# 노드 C
graph['C']['A'] = 4
graph['C']['D'] = 3

# 노드 D
graph['D']['E'] = 1

# 도착점 노드
graph['E'] = {}

비용 테이블

시작점 노드에서 각 해당 노드까지 도달하는데 드는 비용을 비용 테이블에 정리한다. 비용을 모르는 노드의 비용은 무한대로 둔다.

# 무한대
inf = float('inf')

costs = {}

# S 에서 A 까지 도달하는데 드는 비용
costs['A'] = 1

# S 에서 C 까지 도달하는데 드는 비용
costs['C'] = 2

# 아직 비용을 알 수 없는 노드는 무한대로 설정
costs['B'] = inf
costs['D'] = inf
costs['E'] = inf

부모 테이블

어떤 노드에 대하여 그 노드로 도달할 수 있는 노드, 즉, 부모 노드들을 부모 테이블에 정리한다.

parents = {}

# A 의 부모 노드는 S
parents['A'] = 'S'

# C 의 부모 노드도 S
parents['C'] = 'S'

parents['E'] = None

처리된 노드 목록

processed = []

파이썬으로 구현

먼저 가장 비용이 적게드는 노드를 찾아주는 함수를 작성한다.

def find_lowest_cost_node(costs):
    lowest_cost = float('inf')  # 최저 비용
    lowest_cost_node = None  # 최저 비용 노드
    # 비용 테이블에서 노드를 하나씩 돌면서
    for node in costs:
        # 비용 정보를 cost에 저장
        cost = costs[node]
        # 비용 정보가 최저 비용보다 낮고 그 노드가 처리되지 않은 노드일 때
        if cost < lowest_cost and node not in processed:
            # 최저 비용 갱신
            lowest_cost = cost
            # 최저 비용 노드 갱신
            lowest_cost_node = node
    # 최저 비용 노드 리턴
    return lowest_cost_node

node = find_lowest_cost_node(costs)
while node is not None:
    cost = costs[node]
    neighbors = graph[node]
    for n in neighbors.keys():
        new_cost = cost + neighbors[n]
        if costs[n] > new_cost:
            costs[n] = new_cost
            parents[n] = node
    processed.append(node)
    node = find_lowest_cost_node(costs)